I find the solution to a problem found in an XKCD comic involving raptors attacking a human. The goal was to find the optimal action for a human who is surrounded by three raptors positioned in an equilateral triangle. The problem appears in an XKCD comic at https://xkcd.com/135/.

Question 2

Let the human position be $\boldsymbol{h}(t) \in \mathbb{R}^2$ and a raptor’s position $\boldsymbol{r}(t) \in \mathbb{R}^2$.

A raptor’s motion can be modeled as

where if $\boldsymbol{x}=(x,y)$ then we define $\vert \boldsymbol{x}\vert = \sqrt{x^2+y^2}$.

The three raptor’s each satisfy this ODE separately, but the $x$ and $y$ components of a raptor’s motion are coupled, so we have 2-dimensional ODEs.

For simplicity, we assume the human runs in a constant direction and at a constant speed. Thus,

where $\boldsymbol{c} \in \mathbb{R}^2$ is an initial direction and $\boldsymbol{h}(0)$ is the human’s initial position.

We substitute $\boldsymbol{h}(t)$ into equation (1) to obtain $\frac{d \boldsymbol{r}}{dt}=F(t, \boldsymbol{r})$ for some function F (to be defined).

As in the comic, the human is at the center of an equilateral triangle with 20m sidelengths. The human has a top speed of $v_h=6$ m/s. The healthy raptors have a top speed of $v_r=25$ m/s. We’ll assume the injured raptor can run at 20 m/s to make the problem more interesting.

Define the human as “caught” when the raptor is within 0.01 m of the human. Specifically, assume the human starts running at a $56^{\circ}$ angle above the horizontal.

We have $\boldsymbol{h}(0)=(0,0)$ since the human starts at the origin. $v_h=6$, the (max) velocity of the human.

To determine $\boldsymbol{c}$ we have $y=6\sin(56)\approx 4.974$ and $x=6 \cos(56) \approx 3.355$.

\(c= (3.355,4.974)\) so \(|c|= \sqrt{3.355^2+4.974^2}=6\)

Thus, $\boldsymbol{h}(t) = 6t\frac{(3.355,4.974)}{6} = (3.355t,4.974t)$.

So Equation (1) becomes \(\frac{d \boldsymbol{r}}{dt} = F(t, \boldsymbol{r}) = v_r \frac{(3.355t,4.974t)- \boldsymbol{r}(t)}{|(3.355t,4.974t)- \boldsymbol{r}(t)|}\)

import numpy as np
import scipy.integrate
import scipy.interpolate
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

h = lambda t: (3.355*t,4.974*t)

#dr/dt
v_r1 = 20 #velocity of raptor 1
F1 = lambda t,r: v_r1*((3.355*t,4.974*t)-r)/np.sqrt((3.355*t-r[0])**2+(4.974*t-r[1])**2)
v_r = 25 #velocity of uninjured raptor
F = lambda t,r: v_r*((3.355*t,4.974*t)-r)/np.sqrt((3.355*t-r[0])**2+(4.974*t-r[1])**2)

tStart= 0.0
tStop = 5.0
tspan= (tStart, tStop)

r1 = (0,11.547)
r2 = (10,-5.7735)
r3 = (-10,-5.7735)
raptor1 = solve_ivp(F1, tspan, r1, dense_output=True)
raptor2 = solve_ivp(F, tspan, r2, dense_output=True)
raptor3 = solve_ivp(F, tspan, r3, dense_output=True)
print('Success status of IVP solver is: ', raptor1.success)

t = np.linspace(0,1,2000)
# make variable arrays less confusing, do this for each raptor
t_r1 = t
x_r1 = raptor1.sol(t)[0,:]
y_r1 = raptor1.sol(t)[1,:]
...

# Find time human is "caught" by each raptor
def distanceFormula(x1,y1,x2,y2):
    xdiff = np.subtract(x2,x1)
    ydiff = np.subtract(y2,y1)
    distance = np.sqrt(xdiff**2+ydiff**2)
    return distance #this is an nd.array

def raptorEatsHuman(distanceBetween):
    if any(element < 0.01 for element in distanceBetween):
        for element in distanceBetween:
            if element<0.01:
                idx, =  np.where(np.isclose(distanceBetween, element))
#                 timeCaught = float(time[idx])
                return idx #this is a float
    return("Failed.")

# Time Raptor 1 Catches Human, do this for each raptor
x_h1 = h(t_r1)[0]
y_h1 = h(t_r1)[1]
R1_distanceBetween = distanceFormula(x_h1,y_h1, x_r1, y_r1)
index1 = int(raptorEatsHuman(R1_distanceBetween))
timeCaught1 = float(t_r1[index1])
...

timeCaught = np.array([timeCaught1, timeCaught2, timeCaught3])
for i in np.arange(1,4):
    print( f'Time caught by raptor{i:2d}, t = {timeCaught[i-1]:.16}' )

Time caught by raptor 1, t = 0.4772386193096548
Time caught by raptor 2, t = 0.4827413706853426
Time caught by raptor 3, t = 0.6068034017008503

SOLUTION:

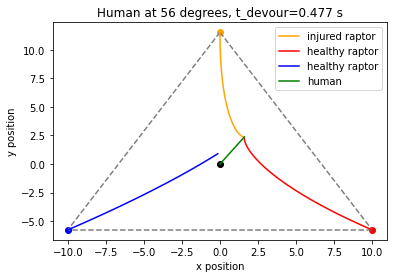
The human is caught by the injured raptor at t = min(timeCaught) = 0.4772386193096548

If the human starts in the center of the triangle and runs at a 56 degree angle above the horizontal, the injured raptor reaches the human first at 𝑡≈0.477 seconds.

Additional interesting questions to consider: 
Optimize the angle for this problem. 
For which top speed of the wounded raptor does the optimal strategy become to run straight at the wounded raptor?